Violin making is a conservative discipline. The vast majority of instruments are copies of previous instruments. When it comes to violins the first place we look is usually the work of Antonio Stradivari. While Strad did make a few violas, common wisdom does not regarded them as well as his violins. So when I was sat down to make a viola I found my options had narrowed down to everything else.
❧ ❧ ❧
The first choice I had to make was size. Most violins are about the same length. It’s a size that works. Violas, however, don’t work. Violas are made in a range of lengths, roughly from 15 to 17 inches. There are two things going on here: First, each model is an attempted compromise between sound and playability. A larger instrument can give a fuller and, importantly, louder sound. Part of the reason that viola concertos are rarer than violin concertos is that the violin is able to project over the orchestra in a way that the viola has trouble with. I swear there is no anti-viola conspiracy at work here; it’s just physics. Basically, the viola is tuned a fifth lower than the violin but is not scaled up proportionally to be a fifth larger.
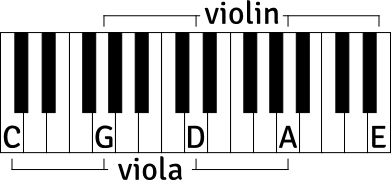
The strings on a violin and viola.
It’s not all bad, though, because this is exactly why the viola sounds the way it does. The unique, and desirable, timbre of the viola—which is often described as “dark” or even “growly”—seems to be the trade-off for a somewhat less powerful instrument. Which isn’t to say that no one has built a violin scaled up to viola tuning, but that’s not a viola.
Building a larger viola can often get you more oomph, but at some point you make it difficult to play for those of us without extra long arms. Trying to play a too big instrument isn’t just uncomfortable (though, who wants to practice hour after hour on a painful instrument?) but can make more virtuosic passages nigh impossible or even lead to injury. Because there is no single good compromise between tone, volume, and playability we instead continue to build a range of violas to suit different players and different needs.
The second thing going on is that there used to be two kinds of violas: tenor and alto1Riley, Maurice W. The History of the Viola. Ann Arbor, MI: Braun-Brumfield, 1980. 12. The larger, tenor, viola has largely fallen out of fashion. There is no clear cut single reason for this. Part of the story is undoubtedly that they are just too big to play comfortably2One could speculate about alternative performance practices such as playing on the arm or even on the lap like a cello, but that doesn’t help the modern violist playing modern repertoire.. Part of the story might also be changes in musical style and needs. But, the details are difficult to trace, in large part because of terminology-confusion, so I’ll leave that for a future post.
As a quick aside I should mention that there are some wacky (esp. non symmetrical) violas designs out there which have been offered over the years as creative solutions. Some of them might even work. I don’t know and that’s all I can say on that topic. On a similar note, while we often talk about viola sizes in terms of back lengths, obviously that’s not the whole story because it’s really about vibrating string length, internal air volume, plate surface area and curvature, and more—all of which generally scale with back length but not necessarily or directly3Which is to say: Dear violists, please don’t focus so much on back length when searching for a new viola. Thank you..
❧ ❧ ❧
For this instrument I—arbitrarily—chose to make something on the smaller end of things. I had access to a technical poster of a G. B. Guadagnini viola with a back length of about 400 mm (~15 ¾″). Ideally one would always chose a model based either on the past experience of having built a number of them, or at least from having heard the original. Unfortunately we often have nothing more than recordings and the traditional knowledge of the violin making community to go off of and are limited by what instruments, posters, and books we have access to.
I had some confidence in this model because Mr. Guadagnini made a bunch of them. In addition to the example from the poster I found two more in the Guadagnini Book, and a fourth online, which seemed enough to establish that this was not a one-off design. Furthermore, they are all from late in his career when he lived in Turin. Guadagnini employed a variety of viola models over the course of his life. These changes might not mean anything. We can never know for certain why a maker made the design changes and choices they did. Today we are driven, mostly, by a desire to optimize certain tonal properties. Of course folks in the 17th and 18th century cared about sound4e.g. Prizer, William F. “Isabella d’Este and Lorenzo da Pavia, ‘Master Instrument-Maker’.” Early Music History 2 (1982):87-118+120-127, but projecting our desires and mindset onto past makers may or may not always be accurate. For example, we can’t know what kind of influence Guadagnini’s patron at the time, Count Ignazio Alessandro Cozio di Salabue, might have had. And lastly, even if the Old Makers were designing in the service of sound, we should still be cautious about the conclusions we draw because of differences in historical set-up, playing style, and possibly acoustical aesthetics. But still, given that Guad kept making this particular model right up to the end of his career I am inclined to believe that he considered them “successful”, whatever that might have meant to him. Hopefully it meant, at least in part, “great sounding”5I doubt it meant “great looking” because these violas are squat and a bit awkward visually. But, here again, aesthetics change over time so we have to be careful..
❧ ❧ ❧
Now that I knew what I was going to copy I had to figure out how to copy it.
Many violin makers pride themselves on making close copies of historical instruments. That does not, however, mean that we all have the same approach in mind. Ask two makers to use the same model as reference and you might end up with three or four very different instruments. Just saying “copy everything, and get it as close as possible to the original” is far too broad to be useful as a guiding principle. To help me narrow it down a bit I use the following sensitizing concepts when thinking about how to approach a copy6None of which are unique, or even original, to me..
My underlying axiom is that I care about sound. I believe that the impetus for using old instruments as the basis for my models is to capture their sound profile. Therefore, what I am trying to copy are all the things related to how they sound.
The first assumption that I make is that instruments are very complicated. Because of this we have to further assume that every minute aspect has the potential to be important for the final sound. Of course, I can use what I have learned—which includes the craft knowledge passed down to me by my teacher, the experiential knowledge from my making, and the scientific knowledge that acoustician and other have produced—to make informed guesses and decisions about what aspects of the instrument are more or less sensitive to being changed. But, I have to be careful because I don’t know everything, I could be wrong, and there could be complex and subtle interactions and knock on effects7There is an even more fundamental assumption at work here, namely that the sound of an instrument is entirely a product of its materiality. Which seems fine to me, but there are ongoing debates in the violin making world about such things as the role of playing-in instruments as well as more esoteric theories about the “magic” of Strad..
My second assumption is that instruments are a product of craft, which is to say that to fully understand them one should look at the process by which, and context in which, they were produced. I believe that it follows that emulating, to the extent practical, the working method of the original maker will help me more accurately capture his end product. First, because by using historical methods and tools I will copy not only the macro features of the instruments but also those micro-features which are “accidental” side effects of particular techniques. And second, because this approach helps me understand the mindset and perspective of the original maker, which in turn helps inform decisions about the model I am trying to copy. The work of people such as Maestro Sacconi, Roger Hargrave, and others—who have not only written extensively about old instruments but also studied the surviving tools of Stradivari and sought to understand how they relate to his making and his instruments—has been invaluable to the violin making community on this front.
And lastly, an important caveat. While I am trying to make a copy, I am not making an identical instrument. I am working with a different piece of wood that has different physical properties (density, stiffness, etc.). Modern set-up is different from historical baroque set-up in ways both small and large (neck set, strings, etc.). The context in which my instrument will live is different (repertoire, performance practice, etc.). And, of course, I am not Mr. Stradivari, or even Guadagnini, but myself. All of which is to say that some deviation from a strict copy will be appropriate and even necessary.
❧ ❧ ❧
Enough theory, here’s how I went about getting ready to make this viola.
I started with figuring out the outline, both because it’s the most obvious feature of what makes a given model that model and because it’s closely tied to where we start when building an instrument. Violins, violas, and cellos are built by bending the ribs around a form, that we call a mold8There are other ways to build a rib structure, but for this post we’re confining ourselves to the Classic Cremonese Working Method [CCWM] since that’s what Guad used [WWGD?].. The outline of the top and back plates will then be based on the resulting rib structure.

Stradivari viola mold, image from The Secrets of Stradivari by Sacconi.
That’s a photo of one of the molds that Mr. Stradivari himself used. Unfortunately, the mold that Guadagnini used for the viola I wanted to copy has not survived. So in order to reconstruct the mold I have to work backwards from the rib-structure. I just want to underline that my interest in the rib-structure here, which is really an interest in the mold that produced it, is a product of my two assumptions from above, and especially of what is known about the Classic Cremonese Working Method [CCWM]; for example, if I thought of copying as primarily a visual endeavor my starting point might be the outline of the plates.
Most of the time we can’t pop the top off a 3– 400 year old instrument and merrily trace the inside of its rib-structure. Usually all we have to work off of are some nice 1:1 photographs, which show the shape of the plates but not the rib-structure since that’s hidden by the overhang.

Overhang is the part of the plate that extends past (i.e. hangs over) the rib structure.
To get at the rib-structure we have a few options. First, we can work off of the plate outline and subtract the overhang + the thickness of the ribs—remember we want the inside of the rib-structure because we are actually after the mold that produced it9Did the CCWM prize the inside mold because they cared about the connection between air-volume and sound? I don’t know, but it’s possible.. Unless we have the instrument in front of us, it’s unlikely that we have that data for every point of the outline. At best we have a few measurements and the hope that there isn’t too much variance—which is more likely to be true of some makers, like Nicolo Amati, than others, like my Guadagnini. Sometimes all we can do is guess based on general knowledge of what kind of measurements that particular maker tended to prefer. Second, we can look at the purfling, which often—but far from always—closely matches the rib-structure. Third, for a select few instruments we have been given the wonderful gift of CT scans. Fourth, for the work of Stradivari, as I mentioned above, we have many of his original molds.
These four approaches don’t exist independently of each other. Each can help inform and refine the others. For example, when scans of the particular instrument we’re after aren’t available, other scans—especially when from the same maker—can help us double check and calibrate our other methods. And looking at the purfling can be an important supplement in areas where the overhang is very worn or erratic. For me, the exact blend of methods I end up relying on is largely driven by what data is available to me.
However, no matter what you do all of these methods run up against some basic limitations. The instruments we are looking at tend to be 3– 400 years old. Any wooden object that old will display, sometimes significant, wear and distortion, especially one that has been prized primarily for its use-value and not just art-value. Even an instrument in pristine condition could be misleading. These are handcrafted objects so human variance always plays a role. The mold does not completely constrain the shape of the rib-structure, and once the rib-structure is removed from the mold further variance is possible. You might say who cares, if you’re making a copy you should copy it warts and all. But, molds were rarely one off designs10Though, it is notable that Stradivari seems to have experimented with different molds more than most. so unless I have strong reason to believe that one specific instrument is significantly more successful than others made off of that mold, it’s probably the maker’s intention, as embodied by the mold, that I am after. Moreover, I too am human and am likely to introduce some variance. If I add my “error” on top of that of Mr. Guadagnini I will likely be even further from my intended goal.
Are we then stuck with an imperfect outline? Not necessarily. Wear, distortion, and human variance don’t happen randomly; each has its own pattern. By studying old instruments we can build a mental model of how instruments tend to change over time and use that—plus our knowledge of the types of shapes and design decisions particular makers tended to make—to make informed decisions about how we might work backwards from what’s in front of us. For example, we can decide that the outline we have is good enough, or that there isn’t enough information or reason to change it one way vs. another, and just go with it. We might conclude that one side of the instrument is more pristine than the other and make a half template, that we then flip to get both sides, thus yielding a symmetric outline. We might chose to make “corrections” to the outline by hand, or with the aid of a compass or french curves. Or we might do what I did for this particular viola: a geometric construction.
But, before I get into what the heck that means two important caveats. One, while I am spending a lot of time in the post on the outline, outline ≠ destiny. There is a lot more to a model than just the rib-structure, such as rib height, ff-hole placement, stop length/vibrating string length, and arching. The outline influences all of these, but it does not completely determine them. And two, at the end of the day the model is only a third of the instrument’s destiny. Instruments are the product of design + material + construction11Which includes set-up!. This post only covers the journey.
❧ ❧ ❧

At its most basic geometric construction is drawing shapes using just a compass and straight edge. These days we mostly think of it as an academic exercise with an interesting history (think Euclid), and some abstract mathematical applications, none of which explains why I would want to use it to generate the outline of my viola. Going off what I’ve written up to now you might expect me to whip out some evidence that Mr. Stradivari sat around in the evening with his trusty compass and doodled new violin designs. No such evidence exists. In fact, there is no direct historical evidence that these techniques were used as part of the classic Cremonese working method.
What we do know is that—as has been demonstrated by the important work of François Denis in his groundbreaking book Traité de Lutherie—one can successfully draw a wide variety of classic Cremonese models using the techniques of geometric construction. Furthermore Stradivari—and presumably others—owned a compass and straight edge12In fact, we have technical drawings in Stradivari’s hand that use compass arcs to locate where the ff-holes on an instrument should go., so at the very least it’s possible that geometric construction was part of their repertoire. Also, there is some evidence that geometric construction was used to design other instruments such as lutes and harpsichords, most notably a 15th century manuscript left to us by Henri Arnaut de Zwolle, inching us from possible towards plausible.
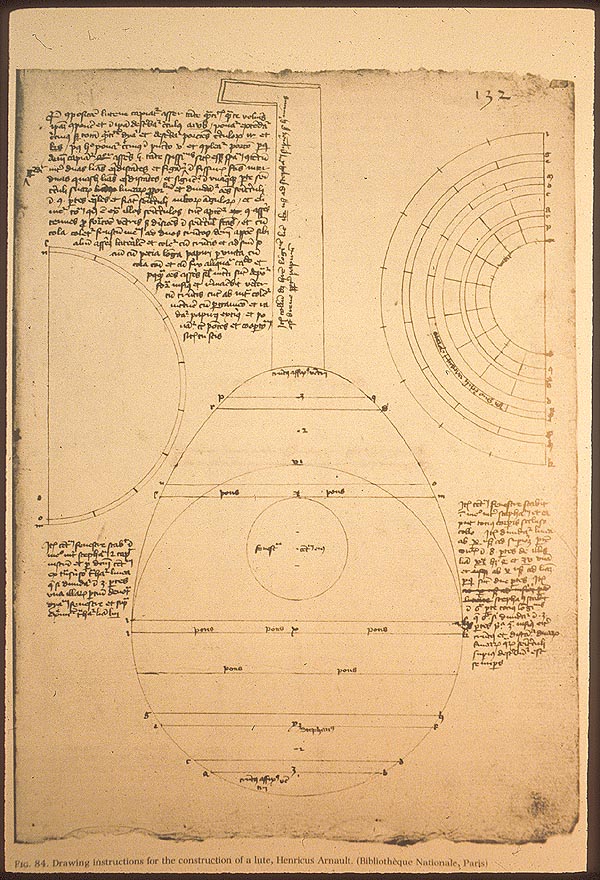
Geometric construction of a lute from de Zwolle’s 15th century manuscript.
More concretely, we know that it was widely used in the fields of architecture and cabinet & furniture making, which may seem like a long way off from violins but this passage from the Roman era Vitruvius’13He’s also the guy behind that famous Da Vinci drawing of a guy inside a circle and a square. 1st century BCE book On Architecture—which was well known and regarded from the 16th century onward, especially in renaissance Italy—will give you an idea of the type of thinking we are about to follow:
On this account the ancient architects, following nature as their guide, and reflecting on the properties of the voice, regulated the true ascent of steps in a theater, and contrived, by musical proportions and mathematical rules, whatever its effect might be on the stage (scena), to make it fall on the ears of the audience in a clear and agreeable manner. Since in brazen or horn wind instruments, by a regulation of the genus, their tones are rendered as clear as those of stringed instruments, so by the application of the laws of harmony, the ancient discovered a method of increasing the power of the voice in a theater.14De architectura, V3§8.
And a little bit later on he write:
For nature has made the divisions of tones, semitones, and tetrachords, and has established those proportions of the intervals, by which workmen are guided in making and assigning their just proportions to instruments.15De architectura, V4§4.
And then he goes on to take a lengthy detour from architecture into music theory, and all the different kinds of chords and scales there are. The key word that shows up in both of these passages is proportion. While the tools of geometric construction may be the compass and straight edge, the real engine is ratios. These days, when we sit down to design something we think in terms of measurements. This needs to be x inches long or y millimeters thick. It’s a system that works particularly well when everything is standardized, e.g. dimensional lumber or screw sizes, like we have been doing since the industrial revolution. But, with geometric construction you start from one measurement—which you can think of more as setting the scale for the whole project—and everything else emerges from that using a system of ratios. These ratios are more than just a cheat sheet to quickly generate a series of measurements. The ways in which the ratios repeat, reappear, and relate to each other is the at the heart of what ultimately produces the design. This idea is behind a lot of classical and baroque architecture. And of course, as Vitruvius alludes, it’s also how music works, which speaks more to a shared theoretical approach than some kind of grand acoustical convergence. Though, that kind of grand convergence is exactly what folks at the time had in mind when they talked about the music of the spheres.
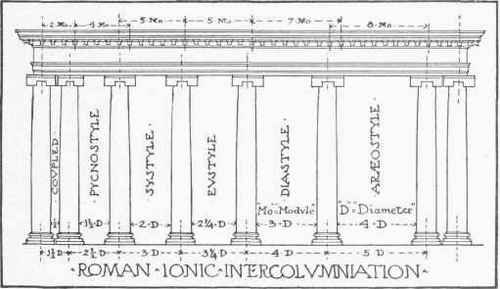
From the Cyclopedia Of Architecture, Carpentry And Building
The take aways here is not that using geometric construction and ratios will magically produce a better designed or sounding violin, but that using these techniques can help us see shapes, and understand the ideas & relationships behind them, in a new way—one that is likely closer to the mentality of the pre-industrial revolution artisans we are trying to copy than our more modern digital caliper approach. One way in which this becomes particularly useful is when studying old instruments and the way that makers built off of and adapted the work of those who went before them. This video from the wonderful maker Kevin Kelly does a great job of that. Be sure to check out all of his other videos about geometric construction, they are a fabulous resource and will give you a good start towards helping you understand how to go about doing a geometric construction of a violin.
❧ ❧ ❧
Armed with all of the above I turned to my viola. As I mentioned above, I worked off of 4 different instruments that I believed to have been constructed on the same mold. First I measured everything I could think of, and—essentially working backwards—tried to uncover the underlying ratios at play. For example I would measure the width of the lower bout and the width of the upper bout and then divide one by the other, hoping that the result came out close to a whole number ratio. Then I would check it on the other three instruments to make sure it wasn’t a fluke.
I want to make a quick aside here about the golden ratio. There is a lot of mysticism caught up with the golden ratio and sacred geometry and how it shows up in nature16That link is to a really awesome video that is really worth watching. that tends to sneak in when one starts down the road of geometric construction. Also, the fact that it happens to create aesthetically pleasing rectangles is nice but not actually the point. So let’s clarify what the golden ratio is. It is the ratio such that ![]() . When using numerals the golden ratio looks pretty hary,
. When using numerals the golden ratio looks pretty hary, ![]() , which makes it seem like any appearance of it must have required great effort. But, when thinking in terms of geometry it’s place becomes simpler and more clear.
, which makes it seem like any appearance of it must have required great effort. But, when thinking in terms of geometry it’s place becomes simpler and more clear.
A big part of what makes the golden ratio so powerful is the way that it builds on itself. Once it’s part of your scheme it will keep cropping up by itself. See how once you have one rectangle whose sides are related to each other by the golden ratio it becomes trivial to construct a second. These types of self perpetuating ratios are precisely the types of interrelated relationships that make geometric construction tick.
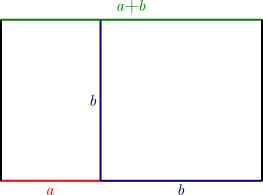
![]()
And getting it to show up the first time is easier than you may think too. First, this concept of building on itself may remind you of the Fibonacci series, which would not be a coincidence. It turns out that the ratio between any two successive numbers in the series will approximate the golden ratio, getting closer as the numbers get bigger. Thus using whole number ratios like ![]() or
or ![]() or even
or even ![]() will give surprisingly close approximation of the golden ratio, especially at the scale of a violin. Second, while calculating the golden ratio requires taking the square root of five and yields a gnarly irrational number, it’s actually very easy to draw through geometric construction, for example:
will give surprisingly close approximation of the golden ratio, especially at the scale of a violin. Second, while calculating the golden ratio requires taking the square root of five and yields a gnarly irrational number, it’s actually very easy to draw through geometric construction, for example:
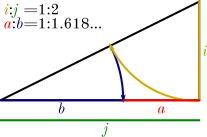
But back to the viola: Once I had amassed a mini-library of ratios the real work began. I had to figure out how these various ratios related to each other and how they might emerge organically from my geometric construction scheme. Mostly this involved drawing outlines over and over trying to get closer and closer to the instruments I was trying to copy. Sometimes I would get something that fit one of them really well but was very off for the others. Then I had to think about what parts of each I trusted the most and why, and where I wanted to try to compromise between them. You can think of it as a sort of forensic reconstruction. The instruments were my crime scene, and I had to come up with a plausible Colonel Mustard with the candlestick. Being slightly to the inside of one of them might be fine if I was still to the outside of another, but clearly being outside of all of them was highly unlikely to be correct. I want to emphasize that this was not just a roundabout way to come up with an average of the four outline, but the application of a technique17As in the greek τέχνη. to see the underlying shapes and harmonies of those outlines.
But, if one thing was off I couldn’t just fix that one thing. Inherent in this technique is that everything affects everything else. Changing one step in the construction leads to a knock on effect that changes every step after it. At one point I thought I had it. I held up my tracing paper to the poster and felt pretty good, went and ate dinner, came back to the workshop, and looked again. I don’t even remember the set of ratios I used for that outline because they were way off. In the end, this is what I came up with—I promise there is a viola outline in all those circles:

And while I have no direct evidence that this is the same outline Guadagnini was after, I feel confident that it’s close. In the end, this approach helped guide me beyond just my outline. My ff-hole placement, stop length, and vibrating string length were all fixed by the same system of geometry and ratios, and even my arching, rib heights, and scroll were informed by the proportions and shapes I had gotten down and dirty with.
Of course, for all of the exacting geometry that went into this instrument it was still my organic hand that did the actual work. I have no desire to make clinical looking instruments, just ones based in the best of violin making’s nearly 500 years of tradition and knowledge. Using geometric construction as my design technique helps me to get a little bit closer to that.

Viola after Guadagnini mid-construction.
References & Notes
| ↑1 | Riley, Maurice W. The History of the Viola. Ann Arbor, MI: Braun-Brumfield, 1980. 12 |
|---|---|
| ↑2 | One could speculate about alternative performance practices such as playing on the arm or even on the lap like a cello, but that doesn’t help the modern violist playing modern repertoire. |
| ↑3 | Which is to say: Dear violists, please don’t focus so much on back length when searching for a new viola. Thank you. |
| ↑4 | e.g. Prizer, William F. “Isabella d’Este and Lorenzo da Pavia, ‘Master Instrument-Maker’.” Early Music History 2 (1982):87-118+120-127 |
| ↑5 | I doubt it meant “great looking” because these violas are squat and a bit awkward visually. But, here again, aesthetics change over time so we have to be careful. |
| ↑6 | None of which are unique, or even original, to me. |
| ↑7 | There is an even more fundamental assumption at work here, namely that the sound of an instrument is entirely a product of its materiality. Which seems fine to me, but there are ongoing debates in the violin making world about such things as the role of playing-in instruments as well as more esoteric theories about the “magic” of Strad. |
| ↑8 | There are other ways to build a rib structure, but for this post we’re confining ourselves to the Classic Cremonese Working Method [CCWM] since that’s what Guad used [WWGD?]. |
| ↑9 | Did the CCWM prize the inside mold because they cared about the connection between air-volume and sound? I don’t know, but it’s possible. |
| ↑10 | Though, it is notable that Stradivari seems to have experimented with different molds more than most. |
| ↑11 | Which includes set-up! |
| ↑12 | In fact, we have technical drawings in Stradivari’s hand that use compass arcs to locate where the ff-holes on an instrument should go. |
| ↑13 | He’s also the guy behind that famous Da Vinci drawing of a guy inside a circle and a square. |
| ↑14 | De architectura, V3§8. |
| ↑15 | De architectura, V4§4. |
| ↑16 | That link is to a really awesome video that is really worth watching. |
| ↑17 | As in the greek τέχνη. |
Tags: design, geometric construction, guadagnini, music history, ratios, stradivari, viola, violin making